Problemas Resueltos: Cinemática (Mecánica)

Problema Número 1:

Un cuerpo de 5 Kg inicialmente en reposo está situado en un plano horizontal sin rozamiento y se aplica una fuerza horizontal y constante de 100 N durante 5 min. Con esa fuerza el cuerpo logra desplazarse 240 m.

a) ¿Qué trabajo se realizó? Expresa el resultado en Kg/m.

b) ¿Cuál es el valor de la potencia mecánica desarrollada?

Solución:

a) W= F x e

W= 100N x 240m

W= 24 x 10(3) N/m= 24 x 10(3) J

1 kg/m= 9,8 J > (1 Kg/m)/(9,8 J)= 1

W=24 x 10(3) J x (1 Kg/m / 9,8 J)= 2,449 x 10(3) Kg/m

b) P= W/t > t= 5 min x (60 seg/1 min)= 300 seg

P= (24 x 10(3) J)/(300 seg)= 80 Watios

Problema Número 2:

Se arrastra una piedra tirando de ella mediante una cuerda que forma con la horizontal un ángulo de 30º, y a la que se aplica una fuerza constante de 40 Kp. ¿Cuánto vale el trabajo realizado en un recorrido de 200m?

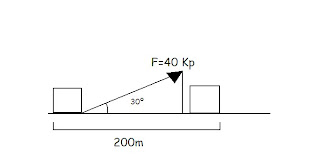
Solución:

W=F x e x cos ángulo

F= 40 Kp > 9,8 N= 1 Kp > 9,8 N/ 1 Kp= 1

F(N)= 40 Kp x (9,8 N/ 1 Kp)= 392 N

W= 392 N x 200 m x cos 30º(0,87)= 68208 J

Problema Número 3:
Mediante un motor de 1/5 caballos de potencia, un cuerpo asciende 10 m en 2 s. ¿Cuál es la masa del cuerpo?

J/seg= Watios > 1 CV= 735 W

P= 1/5 CV (735 W/ 1 CV)= 147 W

147 W= W/ 2s > W= 147 W x 2 seg= 294 J

(294 J)/(9,8 J/Kg)= 3 Kg

Problema número 4:

Un proyectil de 0,4 Kg, atraviesa una pared de 0,5 m de espesor. La velocidad del proyectil al llegar a la pared es de 400 m/s, y al salir de 100 m/s. Calcular:

a)La energia cinética del proyectil al impactar con la pared y al salir de ella.

b)El trabajo realizado por el proyectil

a) Ec = m 1/2 x v(2)

Ec1 = 1/2 (0,4) x (400m/s)(2)

Ec1 = 32000 J

Ec2 = 1/2 (0,4) x (100m/s)(2)

Ec2 = 2000 J

b) W = (Ec2 - Ec1)

W = 2000 - 32000

W = -30000 J

Problema número 5:

Un objeto de 50 Kg se halla a 10 m de altura sobre la azotea de un edificio, cuya altura, respecto al suelo, es de 250 m. ¿Qué energía potencial gravitatoria posee dicho objeto?

EPg = m x g xh

EPg = 50Kg x 9,8M/s(2) x 260 m = 127400 J

Problema numero 6:

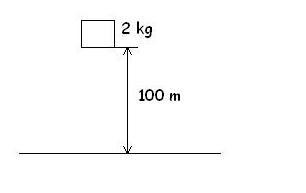
Desde un helicótero a una altura de 100 m sobre la superficie terrestre, se suelta un objeto de 2Kg. Calcula la energía mecánica, cinética y potencial en los puntos siguientes:

a)Antes de soltar el cuerpo

b)Cuando está a 50 m del suelo

c)Cuando está a 10 m del suelo

d)Justo antes de impactar contra el suelo

Nota: g=9,8 m/s(2)

Em = Ep + Ec

a) Em1 = m x g x h

Ep1 = 2 x 9,8 x 100 = 1960 J

Ec1= 0 J

b) Ep2 = 2x 9,8 x 50 = 980 J

Ec2 = 1960 - 980 = 980 J

c)Ep3 = 2 x 9,8 x 10 = 196 J

Ec3 = 1960 - 196 = 1764 J

d)Ep4 = 0 J

Ec4 = 1960 J

Problema número 7:

Un muelle, de longitud 20 cm, se alarga 8 cm al aplicarle una fuerza de 2 N. ¿Qué energía potencial elástica posee en estas condiciones?

Epel > W = 1/2 k x (equis al cuadrado)

Delta de equis = 28 - 20

Delta de equis = 8 cm > x = 0,08 m

W = 1/2 x 25 N/m x (0,08)(2) = 0,08 J

Problema número 8:

Sea la constante K de un resorte igual a 24 N/m, y 4 Kg de la masa del cuerpo. Este se encuentra inicialmente en reposo y el resorte no está alargado. Supongamos que se ejerce sobre el cuerpo una F constante de 10 N y que no existe rozamiento. ¿Cuál será la velocidad del bloque cuando se haya desplazado 0,5 m? Si cesa de actuar la fuerza F cuando el cuerpo se haya desplazado 0,5 m, ¿cuánto seguirá avanzando éste antes de detenerse?

Wp = AEk + AEc

F x e = (Ek2 - Ek1) + (Ec2 - Ec1)

10 x 0,5 = 3 J

Em = Ep + Ec > 5 = 3 + Ec

Ec = 2 J

E = 1/2 x 4 x v(2)

2 = 2 x v(2)

V = 1 m/s

2 + 3 = 5 > 1/2 k x (Equis)(2) = 5 J > x = 0,64 m

Habrá avanzado 0,14 m después de que P cese.

Problema número 9:

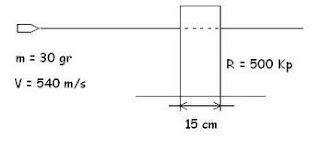
Una bala de 30 gr con velocidad horizontal de 540 m/s atraviesa un poste de madera de 15 cm de espesor. La resistencia opuesta por el poste de madera es de 500 Kp. ¿A qué velocidad saldrá la bala después de haber atravesado el poste?

m = 0,03 Kg

Vo = 540 m/s0,15 m

500 Kp

500 Kp x (9,8N/1Kp) = 4900 N

W = F x e

W = 4900 x 0,15 = 735 J

W = AEc = Ec2 - (1/2 x m x v(2)) = 735 J

Ec2 = 5109 J

V(2) = 5109/0,015

V = 583 m/s

Problema número 10:

Se dispara una bala de 30 gr con un cañón de 1 cm de diámetro y 75 cm de longitud. La velocidad de salida es de 500 m/s. Hallar la energía cinética de la bala y la presión de los gases en la boca del cañón.

Ec = 1/2 x m x v(2)

Ec = 1/2 x 0,03 x 500(2)

Ec = 3750 J > W = F x e

P = F/S > F = 3750/0,75 = 5000 N > S = 3,14 x R

P = 5000/0,00785

P = 63661977 Pa
P = 6366,19 N/m(3)

Problema número 11:

Calcular la potencia necesaria para arrastrar un tren de 100 T por una rampa del 1% de pendiente a la velocidad de 32 Km/h.

32 Km/h x 1000 m/1 km x 1 h/3600 seg = 8,89 m/s

P = W/t = (F x e)/t = F x v

F = m x a > F = 100000 Kg x 9,8 m/s(2)

F = 980000 N

1% > 0,01 = tg alfa

alfa = 0,57º

P = (980000 x sen 0,57) x 8,89

P = 86670,82 W

Problema número 12:

Calcular la potencia de salto de un salto de agua cuyo caudal es de 18.000 M(3)/hora, y cuya altura de caida es de 22 m.

P = W/t > W = F x e > F = m x a

18.000 m(3) x 1000 dm(3)/1 m(3) x 1 l/ 1 dm(3) x 1 Kg/1 l = 1,8 x 10(7) kG

F = 1,8 x 10(7) Kg X 9,8 m/s(2) = 1,764 x 10(8) N

W = 1,764 x 10 (8) N x 22m

W = 3,8808 x 10 (9) J

P = (3,8808 x 10 (9) J)/3600 seg

P = 1,078 x 10(6) W